Fractions are one of those math topics that can make students freeze in their tracks. But why is it so hard for so many students to understand fractions? The problem often lies in a shaky foundation. Many math curriculums that teachers use does not do a good job in building a strong understanding in fractions. Without a strong grasp of the fundamentals, students can easily get lost when fractions start to get more complex. Here’s the good news: YYou can help your students master fractions by building a solid foundation that will carry them through more advanced concepts.
This list will break down the 5 key skills students need to build confidence in fractions, and how you can set them up for success!
1. Understanding What a Fraction Really Is
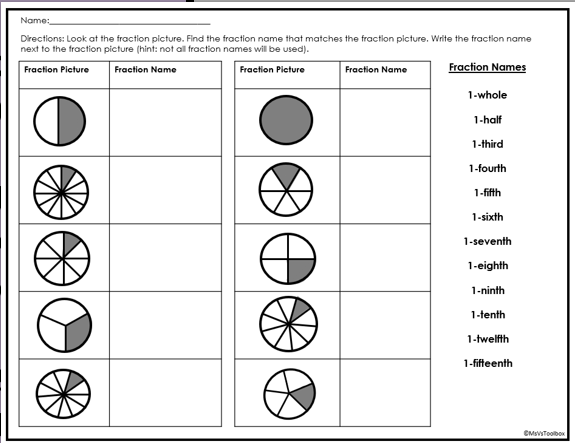
Before diving into operations with fractions, students need to know what a fraction actually represents. A fraction is a part of a whole, but it’s easy for students to confuse fractions with whole numbers.
Why it’s important: If students don’t understand that fractions represent parts of a whole or a set, they’ll struggle to compare, add, or subtract them later.
How to fix it: Use fraction manipulatives. Using fraction manipulatives will help show how a fraction is a part of whole. Color-coded fraction pieces can help them see the part-to-whole relationship clearly.
Provide work pages or design activities that gives students opportunities to use the manipulatives. This exploration is important and key to building their own discovery and conclusions. In my experience, I find that using fraction circle manipulatives is easiest for students to use and understand.
Disclaimer: This post may contain affiliate links, which means I may earn a small commission at no extra cost to you if you make a purchase through these links. I only recommend products and resources that I believe will add value to your teaching experience.
2. Understanding Fractions with the Same Numerator
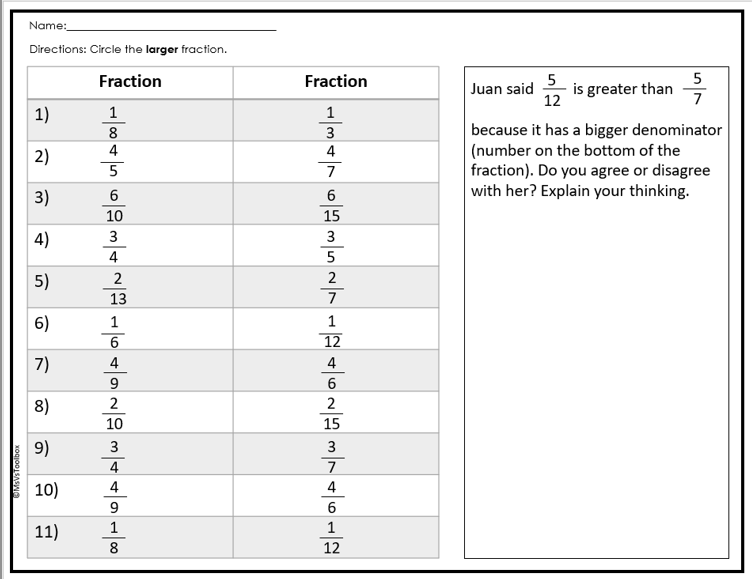
Students need to know and understand that the numerator represents the number of pieces of a whole. If the numerator is the same, everyone gets the same number of pieces.
Why it’s important: Understanding fractions with the same numerator helps students understand the number of pieces they are comparing. If both numerators are the same, then it depends if the piece is small or big.
How to fix it: Start by using fraction models such as fraction circles or bars to compare fractions with the same numerator. For example, showing how 3/4 is larger than 3/6 helps students understand that the same numerator does not necessarily mean the same sized amount.
3. Understanding Fractions with the Same Denominator
Fractions with the same denominator, like 2/4 and 3/4, are easier for students to work with because they have the same size pieces. It’s important for students to recognize that the denominator shows how many equal parts the whole is divided into, and when the denominator is the same, they can simply compare the numerators.
Why it’s important: The denominator indicates the size of each piece.
How to fix it: Use fraction strips or visual models to show how fractions with the same denominator can be compared. You can show that as the denominator increases, the pieces get smaller, making it easier to compare fractions like 1/4 and 1/2 visually.
4. Understanding Fractions Compared to 1/2
One of the most important fraction benchmarks is 1/2. Students need to be able to compare fractions to 1/2, recognizing whether they are larger or smaller. Understanding that 1/2 is the midpoint helps students make sense of other fractions and their relative size.
Why it’s important: Being able to compare fractions to a half or a whole can help students quickly make educated guesses about fractions.
How to fix it: Teach students how to determine if a fraction is equal to a half and discuss why it is equal to 1/2. Make a chart of all fractions that are equal to half to help students understand.
5. Understanding Fractions Compared to 1 Whole
Understanding fractions in relation to a whole is key to mastering fractions. Students need to recognize that fractions like 3/3, 5/5, or 8/8 are equal to 1 whole. Knowing how fractions can represent parts of a whole—and how they add up to a whole—helps students develop a strong foundation.
Why it’s important: When comparing fractions, if students understand that one fraction is closer to a whole while another is closer to a half, they can easily identify which fraction is smaller and which is bigger.
How to fix it: Identify how to know if a fraction is close to a whole. Fractions such as 11/12 or 7/8 are close to a whole. Show and discuss this idea with students.
Conclusion: A Strong Foundation Leads to Fraction Success
By focusing on these 5 key skills, you can help students build a solid understanding of fractions. Once they have a strong foundation in understanding what fractions represent, how they compare to 1/2 and 1 whole, and how to compare fractions with the same numerator or denominator, they’ll be ready to tackle more complex fraction concepts with confidence.
Remember, fractions don’t have to be overwhelming. By teaching students step-by-step and focusing on these foundational skills, you’ll set them up for long-term success in math.
Ready for the next steps? Check out these resources below!